循环不变式[1]
熟练掌握数学归纳法的思路对于程序员来说是相当重要的。例如,要在程序中编写循环处理(loop) 时数学归纳法是非常有用的。
在编写循环时,找到让每次循环都成立的逻辑表达式很重要。这种逻辑表达式称为 循环不变式(loop invariant)。循环不变式相当于用数学归纳法证明的“断言”。
循环不变式用于证明程序的正确性。在编写循环时,思考一下“这个循环的循环不变式是什么”就能减少错误。
光这么说也许不容易理解。我们还是以一个非常简单的例子来讲解循环不变式吧。
代码清单4-2 是用C 语言写的sum 函数,功能是求出数组元素之和。参数array[] 是要求和的对象数组,size 是这个数组的元素数。调用sum 函数,会获得array[0] 至array[size-1] 的size 个元素之和。
代码清单4-2 sum函数,求出数组的元素之和
int sum(int array[], int size){
int k = 0;
int s = 0;
while(k < size){
s = s + array[k];
k = k + 1;
}
return s;
}在sum 函数中使用了简单的 while 循环语句。我们从数学归纳法的角度来看这个循环,得出下述断言M(n)。这个断言就是循环不变式。
断言M ( n ) :数组 array 的前 n 个元素之和,等于变量 s 的值。
我们在程序中成立的断言上标注注释,形成清单4-3 所示代码。
代码清单4-3 在4-2的代码中成立的断言上标注注释
int sum(int array[], int size){
int k = 0;
int s = 0;
// M(0)
while(k < size){
// M(k)
s = s + array[k];
// M(k+1)
k = k + 1;
// M(k)
}
// M(size)
return s;
}在代码清单4-3 的第4 行,s 初始化为0。由此,第5 行的M(0) 成立。M(0) 即为“数组array 的前0 个元素之和等于变量s 的值”。这相当于数学归纳法的步骤1。
图4-8 数学归纳法的步骤1(M(0)成立)

第7 行中,M(k) 成立。然后进行第8 行的处理, 将数组array[k] 的值加入s, 因此M(k+1) 成立。这相当于数学归纳法的步骤2。
图4-9 数学归纳法的步骤2(M(k) M(k+1)成立)
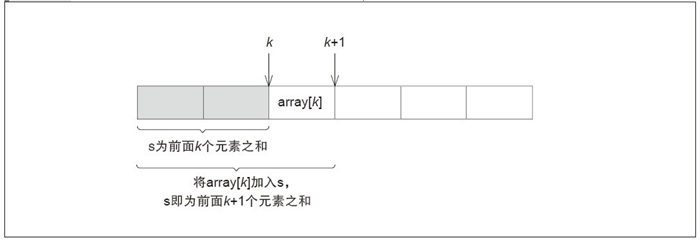
请一定要理解第8 行, s=s+array[k];
意为“在M(k) 成立的前提下,M(k+1) 成立”。
第10 行中k 递增1,所以第11 行的M(k) 成立。这里是为了下一步处理而设定变量k的值。
最后,第13 行的M(size) 成立。因为while 语句中的k 递增了1,而这时一直满足M(k), 走到第13 行时k 和size 的值相等。M(size) 成立说明sum 函数是没有问题的。因此,第14 行return 返回结果。
图4-10 M (size )成立

综上所述,这个循环在k 从0 增加到size 的过程中一直保持循环不变式M(k) 成立。编写循环时,有两个注意点。一个是“达到目的”,还有一个是“适时结束循环”。循环不变式M(k) 就是为了确保“ 达到目的”。而k 从0 到size 递增确保了“适时结束循环”。
代码清单4-4 中,写明了M(k) 成立的同时k 递增的情形。(∧表示“并且”)
代码清单4-4 M (k )成立的同时k递增
int sum(int array[], int size){
int k = 0;
int s = 0;
// M(0) ∧ k ==0
while(k < size){
// M(k) ∧ k < size
s = s + array[k];
// M(k+1) ∧ k < size
k = k + 1;
// M(k) ∧ k ≤ size
}
// M(size) ∧ k == size
return s;
}看了以上循环不变式M(k) 在每次循环时都成立的情形之后,您是否都掌握了呢?
在 《算法导论(第三版)》中,对循环不变式提出了以下三条性质:
|