存储器
概述
存储器的分类
按存储介质分类
半导体分类
磁表面存储器
磁芯存储器
光盘存储器
- 按存取方式分类
随机访问:存取时间与物理地址无关。又分为随机存储器和只读存储器
串行访问:存取时间与物理地址有关。又分为顺序存取存储器(磁带)和直接存取存储器(磁盘)
按在计算机中的作用:
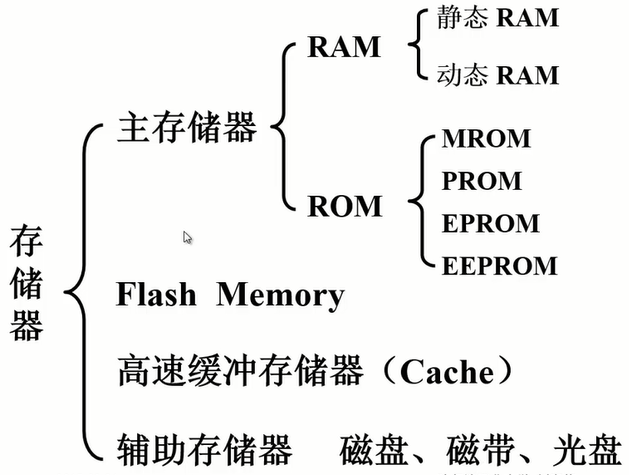
存储器的层次
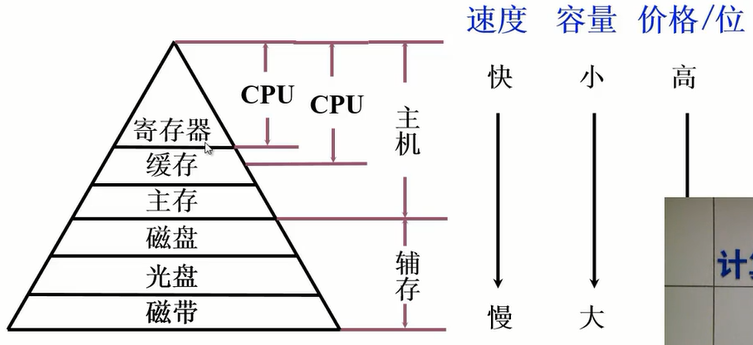
在存储器层次中,两个层次分别为:Cache-主存层次,主存-辅存层次。Cache-主存层次 是为了解决储存速度与CPU速度不匹配的问题,主存-辅存层次是为了解决计算机容量的问题。
半导体存储芯片简介
半导体存储芯片结构如下:
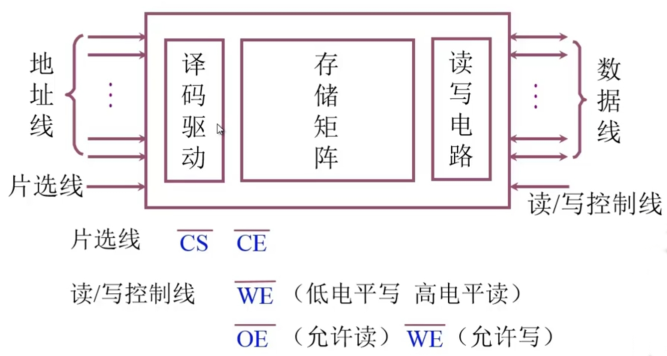
半导体存储芯片的核心结构是存储矩阵,存储结矩阵是由多个可以储存电子信息的元件组成。
片选线 \(\overline{CS}\) 或者 \(\overline{CE}\) 用来表示选择哪一个存储单位。
读写线可以有一条 \(\overline{WE}\) (低电平写,高电平读) 或者两条线: \(\overline{OE}\) (允许读)和 \(\overline{WE}\) (允许写)。上面的横线代表是低电平有效
随机存取存储器
静态 RAM (SRAM):
其基本电路如下:
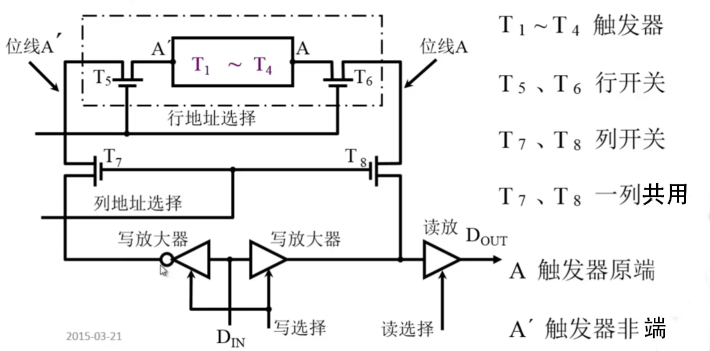
需要注意的是 A 端是触发器的源端, \(A^{\prime}\) 端是触发器的非端。在写入信息的时候,A 端送入原信息, \(A^{\prime}\) 送入取非后的信息。
SRAM的写操作:
在执行写操作的时候,首先使能行地址选择线,然后使能列地址选择线。此时 \(T_5, T_6, T_7, T_8\) 三个触发器全部被选中,电路接通。然后信息从 A 端经过 \(T_6, T_8\) ,再通过读放读出。而 \(A^{\prime}\) 端读出的是与 A 端相反的信息,经过 \(T_5, T_7\) ,然后到写放触发器的时候会被门电路阻止。
SRAM 和 DRAM 的比较:
DRAM | SRAM | |
储存原理 | 电容 | 触发器 |
集成度 | 高 | 低 |
芯片引脚 | 少 | 多 |
功耗 | 小 | 大 |
价格 | 低 | 高 |
速度 | 慢 ,快 | |
刷新 | 有 | 无 |
SRAM 一般用作计算机中的 Cache ,而 DRAM 一般用作主存。
存储器与 CPU 的连接
存储器的拓展
位拓展(增加储存字长):
用两片 \(1K \times 4\) 位的 2114 存储芯片组成 \(1K \times 8\) 位的存储器:
对于存储器而言,其地址线数 = \(\log_2 2^1024 = 10\) 根,数据线数为 8 根。
如图:
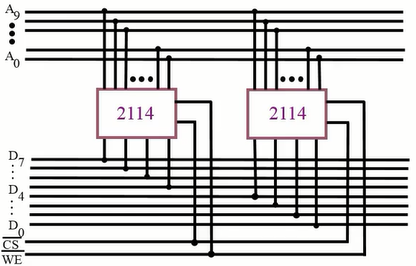
位拓展的关键就是把两个芯片当成一个芯片来用,让这两个芯片同时工作。这意味着两个芯片要用相同的片选线连接。
字拓展(增加储存容量):
用两片 \(1K \times 8\) 储存芯片组成 \(2K \times 8\) 位的存储器:
芯片的地址线为 10 根,而存储器一共有 11 根,多出来的一根线用作片选线,选择两个芯片其中之一。
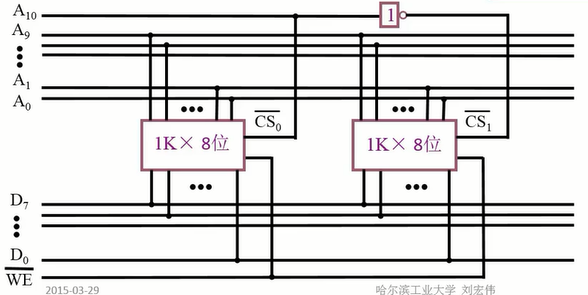
这样,地址 0-00_0000_0000 ~ 0-11_1111_1111 被分配到第一个芯片,地址 1-00_0000_0000 ~ 1-11_1111_1111 被分配到第二个芯片。
字位拓展:
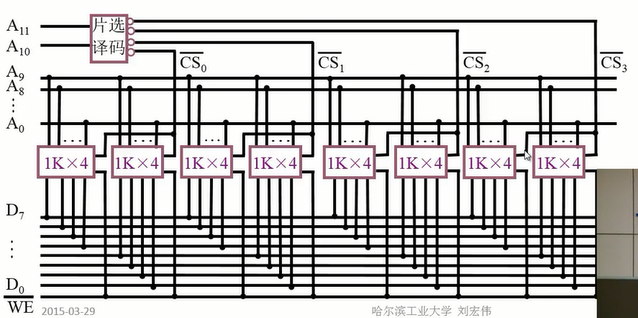
用八片 \(1K \times 4\) 位储存芯片组成 \(4K \times 8\) 位的存储器:
首先用两个 \(1K \times 4\) 位的芯片组成一个 \(1K \times 8\) 两两一组,一共四组。存储器的地址线一共为 \(\log_4\times 2^1024 = 12\) 根,而芯片只有 10 根数据线,多出来的两条线用作片选线,选择四组芯片中的一组。每组的两个芯片的片选线相同。 组与组之间的片选线为互斥关系。
例题
对于一个芯片而言,字数量决定其地址线数,而位数量决定了数据线个数,然后还需要加上片选线和读写控制线(有些芯片读写控制线并做一根)。在使用地址复用技术的时候,地址线数减少了一半,但是片选线分行通选和列通选两根。例如:
[2021 王道机组 P102] 某一 SRAM 芯片其容量为 1024 × 8 位。除电源和接地线外,该芯片的引脚的最小数目为()
21 B. 22 C. 23 D. 24
解析: 地址线数量为: \(log_2{1024}=10\) ,数据线为 8 根,加上片选线和读写控制线,一共为 10 + 8 + 1 + 2 = 21 根。
[2021 王道机组 P103] 某一 DRAM 芯片采用地址复用技术,其容量为 1024×8 位,除电源和接地端外,该芯片的引脚最少数是()(读写控制线为两根)
19 B.17 C. 19 D.21
解析: 由于采用地址复用技术,因此地址线数减少为原来的一半,为: \(\frac{1}{2}log_2{1024} = 5\) ,数据线为 8 根,片选线分为行通选和列通选两根。一共为 5 + 8 + 2 + 2 = 17 根。
[2014 统考真题] 某容量为 256MB 的储存器,由若干 4M×8 位 的 DRAM 芯片构成,该 DRAM 芯片的地址引脚和数据引脚总数是:
19 B. 22 C. 30 D. 36
解析: 需要注意的是这个题考点为芯片的引脚总数,而不是储存器的引脚总数。DRAM 采用地址录用技术其地址限数减少为原来的一半,为: \(\frac{1}{2}log_2{4M} = 11\) ,数据线为 8 根,片选线分为行通选和列通选两根。一共为 11 + 8 = 19 根。
存储器与 CPU 连接的选择
地址线的连接
数据线的连接
读/写命令线的连接
片选线的连接
-
- 合理选择储存芯片
一般而言,保存系统程序、配置信息的使用 ROM ,因为这些信息是不经常改动的。
其他的因素:时序、负载等
数据校验

编码的最小距离(码距):任意两组合法代码之间二进制位数的最小差异
编码的纠错、检错能力都与码距有关。
\(L-1=D+C(D\geq)\)
L:编码的最小距离
D:检测错误的位数
C:纠正错误的位数
海明校验码
海明码是具有两位检错、一位纠错能力的校验码。
海明码是:
海明码采用奇偶校验
海明码采用分组校验
海明码是一种非划分的方式
如图:
假设校验位 + 数据位一共 7 位,则:
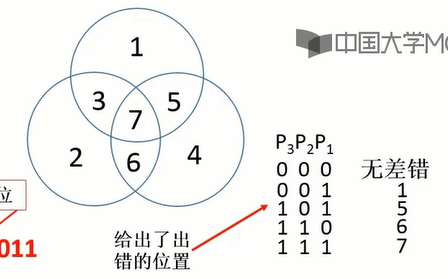
例如:

CRC 校验码
CRC (Cyclic Redundancy Check)) 循环冗余校验码,是以模二相加为基础的四则运算,运算时不考虑 进位和借位 。
对于模二加法来说,由于其加减不借位、不进位,因此等价于异或运算。
CRC 使用模二除法对 生成多项式 进行作商求余,然后将余数附加到原始数据的尾部,得到冗余数据。
生成多项式
其中生成多项式的形式为: \(x^4 + x^2 + x^1 + x^0\) ,该多项式的系数要么为 0 ,要么为 1 。将生成多项式的系数组合起来,就形成了除数: \((10111)_2\) 。生成多项式和余数满足以下关系:
生成多项式的最高次和最低次(即 \(x^k, x^0\) )的系数必定为 1
余数的位数要和多项式的位数相同,位数不够就补 0
任何一位发生错误都使余数不为 0
不同位发生错误应当使余数不同
对余数进行模二除法,应当使余数循环
多项式的位数为其多项式的个数减一,减少的一是将最高位省略。常用的生成多项式如下:
名称 | 生成多项式 | 位数 | 简记形式 | 输入值反转 | 输出值反转 |
CRC-4/ITU | \(x^4+x+x^0\) | 4 | 0x03 | true | true |
CRC-8/ITU | \(x^8+x^2+x^1+x^0\) | 8 | 0x07 | false | false |
CRC-16/IBM | \(x^16+x^15+x^2+x^0\) | 16 | 0x8005 | true | true |
计算过程
对于要校验的信息来说,将要校验的数据左移 k 位,便得到除数。其中 k 位多项式的位数
多项式的系数即为被除数
假设 数据为 \((10110011)_2\) ,生成多项式为 CRC-4/ITU ,则除数为 \((10110011\_0000)_2\) 运算结果如下:

生成的校验码为 \((10110011\_1011)_2\)
该生成的校验码称为 (12, 4) 码,其中 n = 12, k = 4 。 n 为校验码的位数
校验过程
将得到的校验码用生成多项式去除,若数据无误,则余数为 0 ,不同位出错,得到的余数不同。以上述校验码为例,现在假设第 7 位出错,其结果变为:\((11110011\_1011)_2\)
对其重新
提高访存速度的措施
采用高速器件
采用 Cache-主存结构
调整主存结构
调整主存结构
单体多字系统
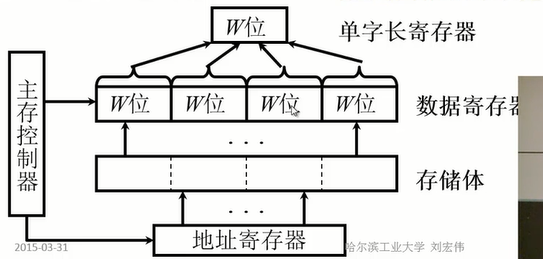
多体并行系统
高位交叉
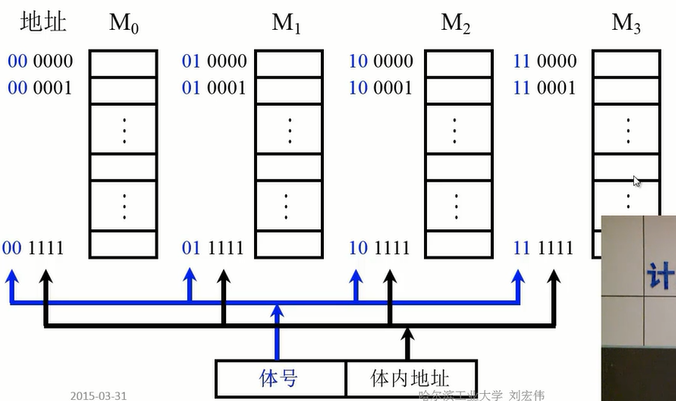
如图,在每一个储存体中都有单独的 MAR 、 MDR 和译码器等 ,将一个地址送入一组储存器,中便完成了高位交叉并行。可以一次性取出一组数据,这种方式主要用于储存容量的拓展
其中体号用于指定选定哪一组储存器,体内地址用于选定同一组储存器中的地址单元
低位交叉
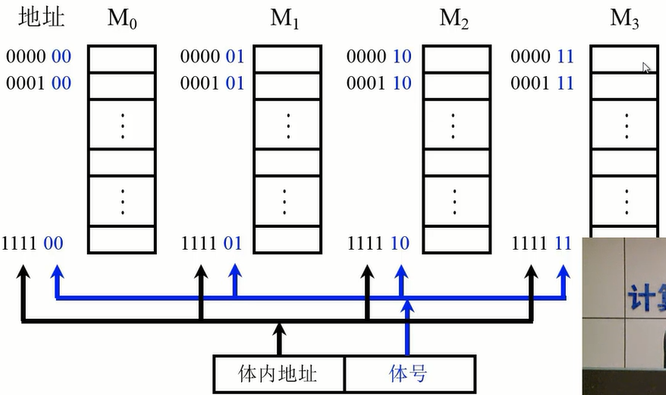
相比于高位交叉,低位交叉在储存数据的时候是按行进行储存的,而不是按列进行储存的。
这样,由于程序是按顺序执行的,那么 Cache 在进行缓冲的时候就会将负载分担到多个储存器中,而不是由一组计算机承担(比如高位交叉)。当储存器准备好数据的时候,就可以交付给CPU,这就是分离式通信
低位交叉的特点:在不改变存储周期的时候,增加储存器的带宽
高性能存储芯片
SDRAM (同步 DRAM): CPU 无需等待 RDRAM 带 Cache 的 DRAM:在 DRAM 芯片中集成了一个由 SRAM 组成的 Cache,有利于猝发式读取
高速缓冲存储器
Cache 的理论依据主要为程序访问的局部性原理:
时间的局部性:当前正在访问的程序的数据,在不久的将来还会再次被访问。该理论的基础是程序中的循环、迭代
空间的局部性:当前正在访问的程序的数据,在不久的将来,与他相邻的数据也会被访问。该理论的基础是程序中的顺序执行
|
Cache 的访问过程如下:
读操作:
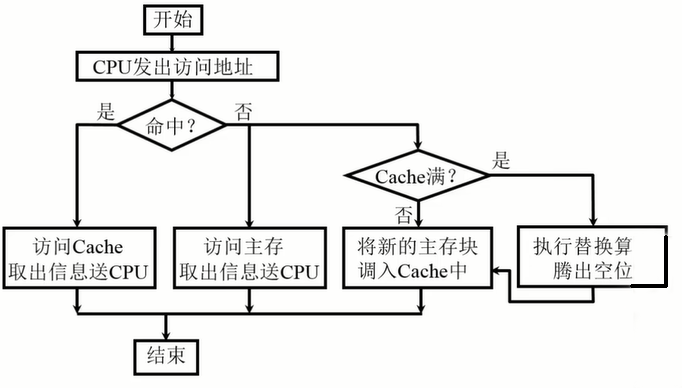
在写的过程中一定要保持 Cache 和主存的一致性问题:
写直达法:在数据写入的时候,既要写入 Cache 也要写入主存。写时间与访问主存时间相同。
写回法:写操作时只把数据写入 Cache 而不写入主存,当 Cache 数据被替换的时候才会写入主存
Cache和主存的地址映射
直接映射:将主存中的大容量地址按照顺序的方法映射到 Cache 中。一般是而言是对地址进行模运算。
优点:结构简单、速度快
缺点:大部分 Cache 空间被浪费、Cache 容易被浪费
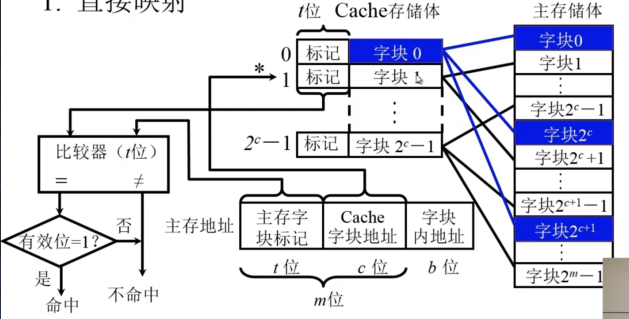
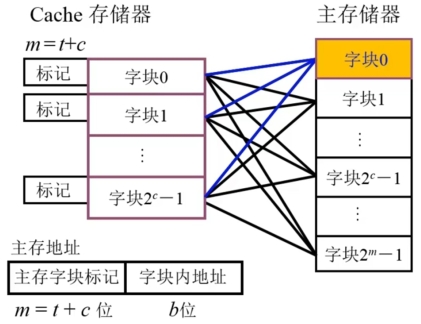
全相联映射
之所以称为全相联映射,是因为主存中的任一个块可以放置在 Cache 中的任一个块中
组相联映射
事实上直接映射和全相联映射走向了内存映射的两个极端。
Cache 结构

如图,其中:
Flag bits 只需要 Valid 位,但是一般也包括 Dirty 位和 Use 位。
Tag 位代表了缓存行的在主存中的实际位置(部分)。
Cache Line 代表了缓存的数据,其长度为主存块的大小。
主存地址结构:

如图,其中:
Tag 的含义与 Cache entry 中的 Tag 含义相同。
Index 代表了对应的 Cache entry 行号。假设 Cache 一共 n 行,则 Index 的长度为 \(log_2{n}\)
Block offset 代表了 Cache entry 中缓存的数据,其长度为 \(log_2b\) 位,其中 b 为 Cache Line 的长度,单位为字节。
Tag 的长度可以计算如下: tag_length = address_length - index_length - block_offset_length |
假设主存大小为 \(2^n\) , Cache 行长为 B 字节,Cache 一共 l 行。则:
主存地址一共 \(\frac{2^n}{B}\) 组,每组对应的 Cache 行号为 \(\frac{2^n}{B}\%l\)
对于组相联映射而言,其
例题:Cache
假设某计算机的储存地址空间大小为 256MB,按字节编址,其数据 Cache 有 8 个 Cache 行,行长为 64B。如果采取直接映射方式,则该数据开启的总容量为?
解析:Cache 总容量为: Cache Line + Tag + Flag.
其中 Cache Line = 64B = 512 bit
Flag 只计算 Valid 位,只有 1 bit.
因此: Cache 的总容量为: \(8\times(1+19+512) = 4256\) bit
Cache 的基本结构
Cache 的改进:
-
- 增加 Cache 的级数
片内 Cache
片外 Cache
-
- 统一缓存和分离缓存
根据指令执行的控制方式,对指令和数据进行统一缓存或者分离缓存
Cache 的工作效率
主存系统的访问效率 \(e=\frac{\text{访问 Cache 的时间}}{\text{平均访问时间}}\)